Posted by Ivan Fratric, Google Project Zero
Intro
Some time ago, I noticed a tweet about an externally reported vulnerability in Skia graphics library (used by Chrome, Firefox and Android, among others). The vulnerability caught my attention for several reasons:
Firstly, I looked at Skia before within the context of finding precision issues, and any bugs in the code I already looked at instantly evoke the “What did I miss?” question in my head.
Secondly, the bug was described as a stack-based buffer overflow, and you don’t see many bugs of this type anymore, especially in web browsers.
And finally, while the bug itself was found by fuzzing and didn’t contain much in the sense of root cause analysis, a part of the fix involved changing the floating point precision from single to double which is something I argued against in the previous blog post on precision issues in graphics libraries.
So I wondered what the root cause was and if the patch really addressed it, or if other variants could be found. As it turned out, there were indeed other variants, resulting in stack and heap out-of-bounds writes in the Chrome renderer.
Geometry for exploit writers
To understand what the issue was, let’s quickly cover some geometry basics we’ll need later. This is all pretty basic stuff, so if you already know some geometry, feel free to skip this section.
A convex polygon is a polygon with a following property: you can take any two points inside the polygon, and if you connect them, the resulting line will be entirely contained within the polygon. A concave polygon is a polygon that is not convex. This is illustrated in the following images:

Image 1: An example of a convex polygon

Image 2: An example of a concave polygon
A polygon is monotone with respect to the Y axis (also called y-monotone) if every horizontal line intersects it at most twice. Another way to describe a y-monotone polygon is: if we traverse the points of the polygon from its topmost to its bottom-most point (or the other way around), the y coordinates of the points we encounter are always going to decrease (or always increase) but never alternate directions. This is illustrated by the following examples:

Image 3: An example of a y-monotone polygon

Image 4: An example of a non-y-monotone polygon
A polygon can also be x-monotone if every vertical line intersects it at most twice. A convex polygon is both x- and y-monotone, but the inverse is not true: A monotone polygon can be concave, as illustrated in Image 3.
All of the concepts above can easily be extended to other curves, not just polygons (which are made entirely from line segments).
A polygon can be transformed by transforming all of its points. A so-called affine transformation is a combination of scaling, skew and translation (note that affine transformation also includes rotation because rotation can be expressed as a combination of scale and skew). Affine transformation has a property that, when it is used to transform a convex shape, the resulting shape must also be convex.
For the readers with a basic knowledge of linear algebra: a transformation can be represented in the form of a matrix, and the transformed coordinates can be computed by multiplying the matrix with a vector representing the original coordinates. Transformations can be combined by multiplying matrices. For example, if you multiply a rotation matrix and a translation matrix, you’ll get a transformation matrix that includes both rotation and translation. Depending on the multiplication order, either rotation or translation is going to be applied first.
The bug
Back to the bug: after analyzing it, I found out that it was triggered by a malformed RRect (a rectangle with curved corners where the user can specify a radius for each corner). In this case, tiny values were used as RRect parameters which caused precision issues when the RRect was converted into a path object (a more general shape representation in Skia which can consist of both line and curve segments). The result of this was, after the RRect was converted to a path and transformed, the resulting shape didn’t look like a RRect at all - the resulting shape was concave.
At the same time Skia assumes that every RRect must be convex and so, when the RRect is converted to a path, it sets the convexity attribute on the path to kConvex_Convexity (for RRects this happens in a helper class SkAutoPathBoundsUpdate).
Why is this a problem? Because Skia has different drawing algorithms, some of which only work for convex paths. And, unfortunately, using algorithms for drawing convex paths when the path is concave can result in memory corruption. This is exactly what happened here.
Skia developers fixed the bug by addressing RRect-specific computations: they increased the precision of some calculations performed when converting RRects to paths and also made sure that any RRect corner with a tiny radius would be treated as if the radius is 0. Possibly (I haven’t checked), this makes sure that converting RRect to a path won’t result in a concave shape.
However, another detail caught my attention:
Initially, when the RRect was converted into a path, it might have been concave, but the concavities were so tiny that they wouldn’t cause any issues when the path was rendered. At some point the path was transformed which caused the concavities to become more pronounced (the path was very clearly concave at this point). And yet, the path was still treated as convex. How could that be?
The answer: The transformation used was an affine transform, and Skia respects the mathematical property that transforming a shape with an affine transform can not change its convexity, and so, when using an affine transform to transform a path, it copies the convexity attribute to the resulting path object.
This means: if we can convince Skia that a path is convex, when in reality it is not, and if we apply any affine transform to the path, the resulting path will also be treated as convex. The affine transform can be crafted so that it enlarges, rotates and positions concavities so that, once the convex drawing algorithm is used on the path, memory corruption issues are triggered.
Additionally (untested) it might be possible that, due to precision errors, computing a transformation itself might introduce tiny concavities when there were none previously. These concavities might then be enlarged in subsequent path transformations.
Unfortunately for computational geometry coders everywhere, accurately determining whether a path is convex or not in floating point precision (regardless if single or double floating point precision is used) is very difficult / almost impossible to do. So, how does Skia do it? Convexity computations in Skia happen in the Convexicator class, where Skia uses several criteria to determine if a path is convex:
- It traverses a path and computes changes of direction. For example, if we follow a path and always turn left (or always turn right), the path must be convex.
- It checks if a path is both x- and y-monotone
When analyzing this Convexicator class, I noticed two cases where a concave paths might pass as convex:
- As can be seen here, any pair of points for which the squared distance does not fit in a 32-bit float (i.e. distance between the points smaller than ~3.74e-23) will be completely ignored. This, of course, includes sequences of points which form concavities.
Note that, in both cases, a path needs to have some larger edges (for which direction can be properly computed) in order to be declared convex, so just having a tiny path is not sufficient. Fortunately, a line is considered convex by Skia, so it is sufficient to have a tiny concave shape and a single point at a sufficient distance away from it for a path to be declared convex.
Alternately, by combining both issues above, one can have tiny concavities along the line, which is a technique I used to create paths that are both small and clearly concave when transformed (Note: the size of the path is often a factor when determining which algorithms can handle which paths).
To make things clearer, let’s see an example of bypassing the convexity check with a polygon that is both x- and y- monotone. Consider the polygon in Image 5 (a) and imagine that the part inside the red circle is much smaller than depicted. Note that this polygon is concave, but it is also both x-monotone and y-monotone. Thus, if the concavity depicted in the red circle is sufficiently small, the polygon is going to be declared convex.
Now, let’s see what we can do with it by applying an affine transform - firstly, we can rotate it and make it non-y-monotone as depicted in Image 5 (b). Having a polygon that is not y-monotone will be very important for triggering memory corruption issues later.
Secondly, we can scale (enlarge) and translate the concavity to fill the whole drawing area, and when the concavity is intersected with the drawing area we’ll end up with something like depicted in Image 5 (c), in which the polygon is clearly concave and the concavity is no longer small.

(a)

(b)

(c)
Image 5: Bypassing the convexity check with a monotone polygon
The walk_convex_edges algorithm
Now that we can bypass the convexity check in various ways, let’s see how it can lead to problems. To understand this, let’s first examine how Skia's algorithm for drawing (filling) convex paths works (code here). Let’s consider an example in Image 6 (a). The first thing Skia does is, it extracts polygon (path) lines (edges) and sorts them according to the coordinates of the topmost point. The sorting order is top-to-bottom, and if two points have the same y coordinate, then the one with a smaller x coordinate goes first. This has been done for the polygon in Image 6 (a) and the numbers next to the edges depict their order. The bottommost edge is ignored because it is fully horizontal and thus not needed (you’ll see why in a moment).
Next, the edges are traversed and the area between them drawn. First, the first two edges (edges 1 and 2) are taken and the area between them is filled from top to bottom - this is the red area in Image 6 (b). After this, edge 1 is “done” and it is replaced by the next edge - edge 3. Now, area between edge 2 and edge 3 is filled (orange area). Next, edge 2 is “done” and is replaced by the next in line: edge 4. Finally, the area between edges 3 and 4 is rendered. Since there are no more edges, the algorithm stops.

(a)

(b)
Image 6: Skia convex path filling algorithm
Note that, in the implementation, the code for rendering areas where both edges are vertical (here) is different than the code for rendering areas where at least one edge is at an angle (here). In the first case, the whole area is rendered in a single call to blitter->blitRect() while in the second case, the area is rendered line-by-line and for each line blitter->blitH() is called. Of special interest here is the local_top variable, essentially keeping track of the next y coordinate to fill. In the case of drawing non-vertical edges, this is simply incremented for every line drawn. In case of vertical lines (drawing a rectangle), after the rectangle is drawn, local_top is set based on the coordinates of the current edge pair. This difference in behavior is going to be useful later.
One interesting observation about this algorithm is that it would not only work correctly for convex paths - it would work correctly for all paths that are y-monotone. Using it for y-monotone paths would also have another benefit: Checking if a path is y-monotone could be performed faster and more accurately than checking if a path is convex.
Variant 1
Now, let’s see how drawing concave paths using this algorithm can lead to problems. As the first example, consider the polygon in Image 7 (a) with the edge ordering marked.
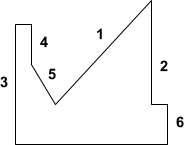
(a)

(b)
Image 7: An example of a concave path that causes problem in Skia if rendered as convex
Image 7 (b) shows how the shape is rendered. First, a large red area between edges 1 and 2 is rendered. At this point, both edges 1 and 2 are done, and the orange rectangular area between areas 3 and 4 is rendered next. The purpose of this rectangular area is simply to reset the local_top variable to its correct value (here), otherwise local_top would just continue increasing for every line drawn. Next, the green area between edges 3 and 5 is drawn - and this causes problems. Why?
Because Skia expects to always draw pixels in a top-to-bottom, left-to right order, e.g. point (x, y) = (1, 1) is always going to be drawn before (1, 2) and (1, 1) is also going to be always drawn before (2, 1).
However, in the example above, the area between edges 1 and 2 will have (partially) the same y values as the area between edges 3 and 5. The second area is going to be drawn, well, second, and yet it contains a subset of same y coordinates and lower x coordinates than the first region.
Now let’s see how this leads to memory corruption. In the original bug, a concave (but presumed convex) path was used as a clipping region (every subsequent draw call draws only inside the clipping region). When setting a path as a clipping region, it also gets “drawn”, but instead of drawing pixels on the screen, they just get saved so they could be intersected with what gets drawn afterwards. The pixels are saved in SkRgnBuilder::blitH and actually, individual pixels aren't saved but instead the entire range of pixels (from x to x + width at height y) gets stored at once to save space. These ranges - you guessed it - also depend on the correct drawing order as can be seen here (among other places).
Now let’s see what happens when a second path is drawn inside a clipping region with incorrect ordering. If antialiasing is turned on when drawing the second path, SkRgnClipBlitter::blitAntiH gets called for every range drawn. This function needs to intersect the clip region ranges with the range being drawn and only output the pixels that are present in both. For that purpose, it gets the clipping ranges that intersect the line being drawn one by one and processes them. SkRegion::Spanerator::next is used to return the next clipping range.
Let’s assume the clipping region for the y coordinate currently drawn has the ranges [start x, end x] = [10, 20] and [0, 2] and the line being drawn is [15,16]. Let’s also consider the following snippet of code from SkRegion::Spanerator::next:
if (runs[0] >= fRight) {
fDone = true;
return false;
}
SkASSERT(runs[1] > fLeft);
if (left) {
*left = SkMax32(fLeft, runs[0]);
}
if (right) {
*right = SkMin32(fRight, runs[1]);
}
fRuns = runs + 2;
return true;
where left and right are the output pointers, fLeft and fRight are going to be left and right x value of the line being drawn (15 and 16 respectively), while runs is a pointer to clipping region ranges that gets incremented for every iteration. For the first clipping line [10, 20] this is going to work correctly, but let’s see what happens for the range [0, 2]. Firstly, the part
if (runs[0] >= fRight) {
fDone = true;
return false;
}
is supposed to stop the algorithm, but due to incorrect ordering, it does not work (16 >= 0 is false). Next, left is computed as Max(15, 0) = 15 and right as Min(16, 2) = 2. Note how left is larger than right. This is going to result in calling SkAlphaRuns::Break with a negative count argument on the line,
SkAlphaRuns::Break((int16_t*)runs, (uint8_t*)aa, left - x, right - left);
x = count;
...
alpha[x] = alpha[0];
Why did this result in out-of-bounds write on the stack? Because, in the case of drawing only two pixels, the range arrays passed to SkRgnClipBlitter::blitAntiH and subsequently SkAlphaRuns::Break are allocated on stack in SkBlitter::blitAntiH2 here.
Triggering the issue in a browser
This is great - we have a stack out-of-bounds write in Skia, but can we trigger this in Chrome? In general, in order to trigger the bug, the following conditions must be met:
- We control a path (SkPath) object
- Something must be done to the path object that computes its convexity
- The same path must be transformed and filled / set as a clip region
My initial idea was to use a CanvasRenderingContext2D API and render a path twice: once without any transform just to establish its convexity and a second time with a transformation applied to the CanvasRenderingContext2D object.
Unfortunately, this approach won’t work - when drawing a path, Skia is going to copy it before applying a transformation, even if there is effectively no transformation set (the transformation matrix is an identity matrix). So the convexity property is going to be set on a copy of the path and not the one we get to keep the reference to.
Additionally, Chrome itself makes a copy of the path object when calling any canvas functions that cause a path to be drawn, and all the other functions we can call with a path object as an argument do not check its convexity.
However, I noticed Chrome canvas still draws my convex/concave paths incorrectly - even if I just draw them once. So what is going on? As it turns out, when drawing a path using Chrome canvas, the path won’t be drawn immediately. Instead, Chrome just records the draw path operation using RecordPaintCanvas and all such draw operations will be executed together, at a later time. When a DrawPathOp object (representing a path drawing operation) is created, among other things, it is going to check if the path is “slow”, and one of the criteria for this is path convexity:
int DrawPathOp::CountSlowPaths() const {
if (!flags.isAntiAlias() || path.isConvex())
return 0;
…
}
All of this happens before the path is transformed, so we seemingly have a perfect scenario: We control a path, its convexity is checked, and the same path object later gets transformed and rendered.
The second problem with canvas is that, in the previously described approach to converting the issue to memory corruption, we relied on SkRgnBuilder, which is only used when a clip region has antialiasing turned off, while everything in Chrome canvas is going to be drawn with antialiasing on. Chrome also implements the OffscreenCanvas API which sets clip antialiasing to off (I’m not sure if this is deliberate or a bug), but OffscreenCanvas does not use RecordPaintCanvas and instead draws everything immediately.
So the best way forward seemed to be to find some other variants of turning convexity issues into memory corruption, ones that would work with antialiasing on for all operations.
Variant 2
As it happens, Skia implements three different algorithms for path drawing with antialiasing on and one of these (SkScan::SAAFillPath, using supersampled antialiasing) uses essentially the same filling algorithm we analyzed before. Unfortunately, this does not mean we can get to the same buffer overflow as before - as mentioned before SkRgnBuilder / SkRgnClipBlitter are not used with antialiasing on. However, we have other options.
If we simply fill the path (no clip region needed this time) with the correct algorithm, SuperBlitter::blitH is going to be called without respecting the top-to-bottom, left-to-right drawing order. SuperBlitter::blitH calls SkAlphaRuns::add and as the last argument, it passes the rightmost x coordinate we have drawn so far. This is subtracted from the currently drawn x coordinate on the line:
x -= offsetX;
And if x is smaller than something we drew already (for the same y coordinate) it becomes negative. This is of course exactly what happens when drawing pixels out of Skia expected order.
The result of this is calling SkAlphaRuns::Break with a negative “x” argument. This skips the entire first part of the function (the “while (x > 0)” loop), and continues to the second part:
runs = next_runs;
alpha = next_alpha;
x = count;
for (;;) {
int n = runs[0];
SkASSERT(n > 0);
if (x < n) {
alpha[x] = alpha[0];
runs[0] = SkToS16(x);
runs[x] = SkToS16(n - x);
break;
}
x -= n;
if (x <= 0) {
break;
}
runs += n;
alpha += n;
}
Here, x gets overwritten with count, but the problem is that runs[0] is not going to be initialized (the first part of the function is supposed to initialize it), so in
int n = runs[0];
an uninitialized variable gets read into n and is used as an offset into arrays, which can result in both out-of-bounds read and out-of-bounds write when the following lines are executed:
runs += n;
alpha += n;
alpha[x] = alpha[0];
runs[0] = SkToS16(x);
runs[x] = SkToS16(n - x);
The shape needed to trigger this is depicted in image 8 (a).

(a)
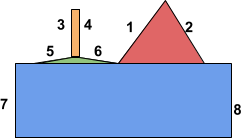
(b)
Image 8: Shape used to trigger variant 2 in Chrome
This shape is similar to the one previously depicted, but there are some differences, namely:
- We must render two ranges for the same y coordinate immediately one after another, where the second range is going to be to the left of the first range. This is accomplished by making the rectangular area between edges 3 and 4 (orange in Image 8 (b)) less than a pixel wide (so it does not in fact output anything) and making the green area between edges 5 and 6 (green in the image) only a single pixel high.
- The second range for the same y must not start at x = 0. This is accomplished by edge 5 ending a bit away from the left side of the image bounds.
Variant 3
Uninitialized variable bug in a browser is nice, but not as nice as a stack out-of-bounds write, so I looked for more variants. For the next and final one, the path we need is a bit more complicated and can be seen in Image 9 (a) (note that the path is self-intersecting).

(a)
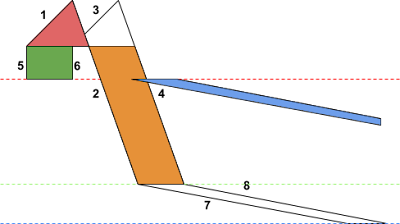
(b)
Image 9: A shape used to trigger a stack buffer overflow in Chrome
Let’s see what happens in this one (assume the same drawing algorithm is used as before): First, edges 1, 2, 3 and 4 are handled. This part is drawn incorrectly (only red and orange areas in Image 9 (b) are filled), but the details aren’t relevant for triggering the bug. For now, just note that edges 2 and 4 terminate at the same height, so when they are done, edges 2 and 4 are both replaced with edges 5 and 6. The purpose of edges 5 and 6 is once again to reset the local_top variable - it will be set to the height shown as the red dotted line in the image. Now, edge 5 and 6 will both get replaced with edges 7 and 8 - and here is the issue: Edges 7 and 8 are not going to be drawn for y coordinates between the green and blue line, as they are supposed to. Instead, they are going to be rendered all the way from the red line to the blue line. Note the very low steepness of edges 7 and 8 - for every line, the x coordinates to draw to are going to be significantly increased and, given that they are going to be drawn in a larger number of iterations than intended, the x coordinate will eventually spill past the image bounds.
This causes a stack out-of-bounds write if a path is drawn using SkScan::SAAFillPath algorithm with MaskSuperBlitter. MaskSuperBlitter can only handle very small paths (up to 32x32 pixels) and contains a fixed-size buffer that is going to be filled with 8-bit opacity for each pixel of the path region. Since MaskSuperBlitter is a local variable in SkScan::SAAFillPath, the (fixed-size) buffer is going to be allocated on the stack. When the path above is drawn, there aren’t any bounds checks on the opacity buffer (there are only debug asserts here and here), which leads to an out-of bounds write on the stack. Specifically (due to how opacity buffer works) we can increment values on the stack past the end of the buffer by a small amount.
This variant is again triggerable in Chrome by simply drawing a path to the Canvas and gives us a pretty nice primitive for exploitation - note that this is not a linear overflow and offsets involved can be controlled by the slope of edges 7 and 8. The PoC can be seen here - most of it is just setting up the path coordinates so that the path is initially declared convex and at the same time small enough so that MaskSuperBlitter can render it.
How to make the shape needed to trigger the bug appear convex to Skia but also fit in 32x32 pixels? Note that the shape is already x-monotone. Now assume we squash it in the y direction until it becomes (almost) a line lying on the x axis. It is still not y-monotone because there are tiny shifts in y direction along the line - but if we skew (or rotate) it just a tiny amount, so that it is no longer parallel to the x axis, it also becomes y-monotone. The only parts we can’t make monotone are vertical edges (edges 5 and 6), but if you squashed the shape sufficiently they become so short that their square length does not fit in a float and are ignored by the Skia convexity test. This is illustrated in Image 10. In reality these steps need to be followed in reverse, as we start with a shape that needs to pass the Skia convexity test and then transform it to the shape depicted in Image 9.

(a)

(b)

(c)
Image 10: Making the shape from Image 9 appear convex, (a) original shape, (b) shape after y-scale, (c) shape after y-scale rotation
On fixing the issue
Initially, Skia developers attempted to fix the issue by not propagating convexity information after the transformation, but only in some cases. Specifically, the convexity was still propagated if the transformation consisted only of scale and translation. Such a fix is insufficient because very small concavities (where square distance between points is too small to fit in a 32-bit float) could still be enlarged using only scale transformation and could form shapes that would trigger memory corruption issues.
After talking to the Skia developers, a stronger patch was created, modifying the convex drawing algorithm in a way that passing concave shapes to it won’t result in memory corruption, but rather in returning from the draw operation early. This patch shipped, along with other improvements, in Chrome 72.
It isn’t uncommon that an initial fix for a vulnerability is insufficient. But the saving grace for Skia, Chrome and most open source projects is that the bug reporter can see the fix immediately when it’s created and point out the potential drawbacks. Unfortunately, this isn’t the case for many closed-source projects or even open-sourced projects where the bug fixing process is opaque to the reporter, which caused mishaps in the past. However, regardless of the vendor, we at Project Zero are happy to receive information on the fixes early and comment on them before they are released to the public.
Conclusion
There are several things worth highlighting about this bug. Firstly, computational geometry is hard. Seriously. I have some experience with it and, while I can’t say I’m an expert I know that much at least. Handling all the special cases correctly is a pain, even without considering security issues. And doing it using floating point arithmetic might as well be impossible. If I was writing a graphics library, I would convert floats to fixed-point precision as soon as possible and wouldn’t trust anything computed based on floating-point arithmetic at all.
Secondly, the issue highlights the importance of doing variant analysis - I discovered it based on a public bug report and other people could have done the same.
Thirdly, it highlights the importance of defense-in-depth. The latest patch makes sure that drawing a concave path with convex path algorithms won’t result in memory corruption, which also addresses unknown variants of convexity issues. If this was implemented immediately after the initial report, Project Zero would now have one blog post less :-)
Image 3 is not x-monotone. If you rotate it a little, it could be, but it's not as you present it.
ReplyDeleteVery nice post, thanks! One nit:
ReplyDelete"A convex polygon is both x- and y-monotone, but the inverse is not true: A monotone polygon can be concave, as illustrated in Image 3."
Image 3 is not a valid example for falsifying the converse implication, because it isn't x-monotone. You can instead spoil 5a which is both x and y-monotone but not convex.